A latent heat model of vaporisation of water considering the critical temperature.

The model uses an equation for a general expression of the latent heat of vaporisation of water in the vicinity of and far away from the critical temperature, which was presented by Torquato and Stell in [38].

Denoting the critical temperature as \(T_c\), and introducing a dimensionless variable \(\tau=(T_c-T)/T_c\) associated with temperature \(T\), the equation is given by

\[ L(\tau) = a_1 \tau^{\beta}+a_2 \tau^{\beta+\Delta} +a_4 \tau^{1-\alpha+\beta} +\sum_{n=1}^{M}(b_n \tau^n),\,\text{[kJ/kg]}, \]

where the parameters of \(b_n\) are obtained by the least square method by fitting the equation with the experiment data.

In this model, the parameter set of \(M=5\) is taken for a high accuracy. All parameters are given below:

\(\alpha=1/8,\,\beta=1/3,\, \Delta=0.79-\beta\),
\(a_1=1989.41582,\, a_2=11178.45586, a_4=26923.68994\),
\(b_n:=\{-28989.28947, -19797.03646, 28403.32283, -30382.306422, 15210.380\}\).

The critical temperature is 373.92 \(^{\circ}\)C.

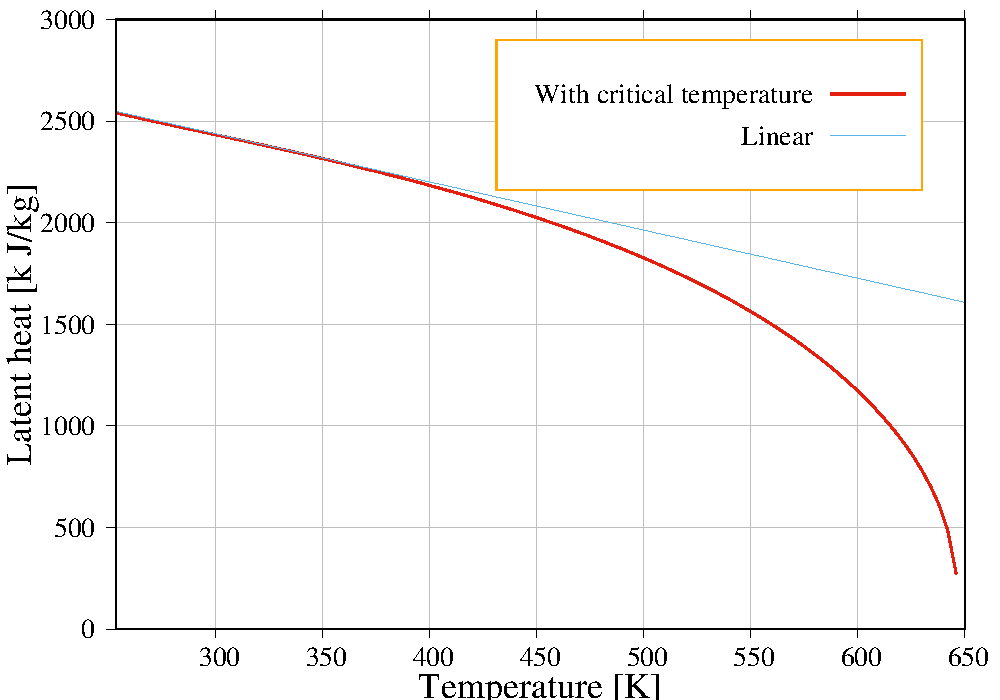
A comparison of this model with the model of MaterialPropertyLib::LinearWaterVapourLatentHeat is given in the following figure.

Child parameters, attributes and cases

Additional info

From MaterialLib/MPL/Properties/Enthalpy/CreateWaterVapourLatentHeatWithCriticalTemperature.cpp line 32

This is a required parameter.
Expanded tag path: NONEXISTENT.property.WaterVapourLatentHeatWithCriticalTemperature
Go to source code: → ogs/ogs/master

Used in the following test data files

Used in no end-to-end test cases.