Assemble and solve the equation system.
239 auto& minus_delta_x =
245 bool error_norms_met =
false;
258 double time_dirichlet = 0.0;
261 time_iteration.
start();
263 timer_dirichlet.
start();
264 sys.computeKnownSolutions(*x[process_id], process_id);
265 sys.applyKnownSolutions(*x[process_id]);
266 time_dirichlet += timer_dirichlet.
elapsed();
268 sys.preIteration(iteration, *x[process_id]);
271 time_assembly.
start();
274 sys.assemble(x, x_prev, process_id);
276 catch (AssemblyException
const& e)
278 ERR(
"Abort nonlinear iteration. Repeating timestep. Reason: {:s}",
280 error_norms_met =
false;
284 sys.getResidual(*x[process_id], *x_prev[process_id], res);
286 INFO(
"[time] Assembly took {:g} s.", time_assembly.
elapsed());
292 minus_delta_x.setZero();
294 timer_dirichlet.
start();
295 sys.applyKnownSolutionsNewton(J, res, minus_delta_x);
296 time_dirichlet += timer_dirichlet.
elapsed();
297 INFO(
"[time] Applying Dirichlet BCs took {:g} s.", time_dirichlet);
305 time_linear_solver.
start();
307 INFO(
"[time] Linear solver took {:g} s.", time_linear_solver.
elapsed());
309 if (!iteration_succeeded)
311 ERR(
"Newton: The linear solver failed.");
320 std::vector<GlobalVector*> x_new{x};
326 if (postIterationCallback)
328 postIterationCallback(iteration, x_new);
331 switch (sys.postIteration(*x_new[process_id]))
336 ERR(
"Newton: The postIteration() hook reported a "
337 "non-recoverable error.");
338 iteration_succeeded =
false;
342 "Newton: The postIteration() hook decided that this "
344 " has to be repeated.");
357 if (!iteration_succeeded)
360 error_norms_met =
false;
364 if (sys.isLinear()) {
365 error_norms_met =
true;
376 INFO(
"[time] Iteration #{:d} took {:g} s.", iteration,
394 ERR(
"Newton: Could not solve the given nonlinear system within {:d} "
404 return {error_norms_met, iteration};
void INFO(char const *fmt, Args const &... args)
void ERR(char const *fmt, Args const &... args)
double elapsed() const
Get the elapsed time in seconds.
void start()
Start the timer.
bool solve(EigenMatrix &A, EigenVector &b, EigenVector &x)
virtual void preFirstIteration()
virtual void checkResidual(GlobalVector const &residual)=0
Check if the residual satisfies the convergence criterion.
virtual bool hasResidualCheck() const =0
virtual bool isSatisfied() const
Tell if the convergence criterion is satisfied.
virtual void checkDeltaX(GlobalVector const &minus_delta_x, GlobalVector const &x)=0
virtual bool hasDeltaXCheck() const =0
virtual void releaseMatrix(GlobalMatrix const &A)=0
virtual GlobalMatrix & getMatrix()=0
Get an uninitialized matrix.
std::size_t _J_id
ID of the Jacobian matrix.
std::size_t _x_new_id
ID of the vector storing .
std::size_t _res_id
ID of the residual vector.
std::size_t _minus_delta_x_id
ID of the vector.
void axpy(PETScVector &y, double const a, PETScVector const &x)
void copy(PETScVector const &x, PETScVector &y)
static NUMLIB_EXPORT MatrixProvider & provider


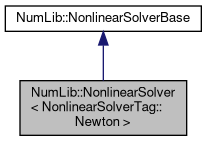
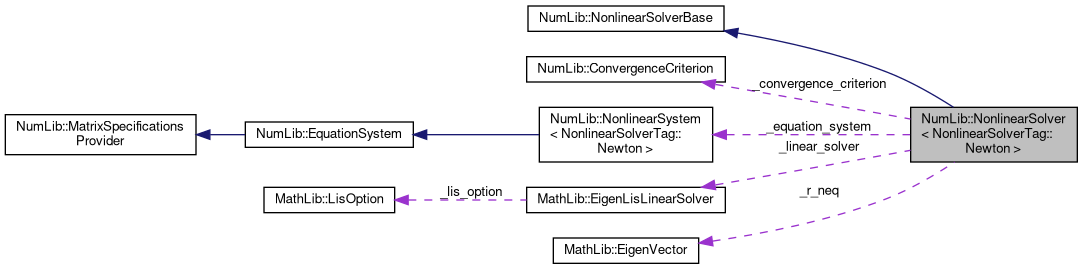
 Public Member Functions inherited from NumLib::NonlinearSolverBase
Public Member Functions inherited from NumLib::NonlinearSolverBase